complex() function do complex number calculations.

complex(length.out = 0, real = numeric(), imaginary = numeric(),
modulus = 1, argument = 0)
as.complex(x, ...)
is.complex(x)
Re(z)
Im(z)
Mod(z)
Arg(z)
Conj(z)

length.out: numeric. Desired length of the output vector, inputs being recycled as needed
real: numeric vector
imaginary: numeric vector
modulus: numberic vector
argument:
x, z: complex object
...

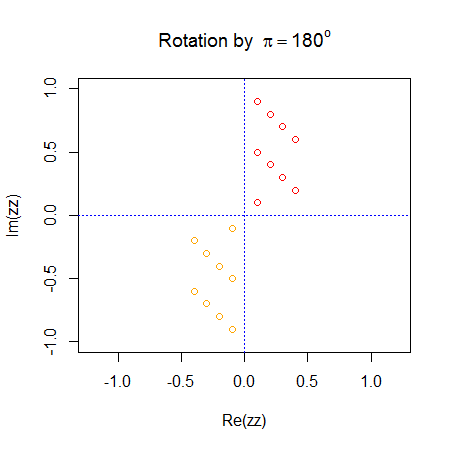
> require(graphics)
> 0i ^ (-3:3)
[1] Inf+0i Inf+0i Inf+0i   1+0i   0+0i   0+0i   0+0i
> matrix(1i^ (-6:5), nrow=4) #- all columns are the same
      [,1]  [,2]  [,3]
[1,] -1+0i -1+0i -1+0i
[2,]  0-1i  0-1i  0-1i
[3,]  1+0i  1+0i  1+0i
[4,]  0+1i  0+1i  0+1i
> 0 ^ 1i # a complex NaN
[1] NaN+NaNi
## create a complex normal vector
> z <- complex(real = stats::rnorm(100), imaginary = stats::rnorm(100))
## or also (less efficiently):
> z
  [1]  0.4058760+0.9050012i -0.8377527-0.2545470i
[3] -1.5847845+3.0573032i -0.7793139-1.5311944i
[5]  0.0620261+0.9123234i  2.1555988-0.7908964i
......
> z2 <- 1:2 + 1i*(8:9)
## The Arg(.) is an angle:
[1] 1+8i 2+9i
> zz <- (rep(1:4,len=9) + 1i*(9:1))/10
> zz
[1] 0.1+0.9i 0.2+0.8i 0.3+0.7i 0.4+0.6i
[5] 0.1+0.5i 0.2+0.4i 0.3+0.3i 0.4+0.2i
[9] 0.1+0.1i
> zz.shift <- complex(modulus = Mod(zz), argument= Arg(zz) + pi)
> zz.shift
[1] -0.1-0.9i -0.2-0.8i -0.3-0.7i
[4] -0.4-0.6i -0.1-0.5i -0.2-0.4i
[7] -0.3-0.3i -0.4-0.2i -0.1-0.1i
> plot(zz, xlim=c(-1,1), ylim=c(-1,1), col="red", asp = 1,
main = expression(paste("Rotation by "," ", pi == 180^o)))
> abline(h=0,v=0, col="blue", lty=3)
> points(zz.shift, col="orange")