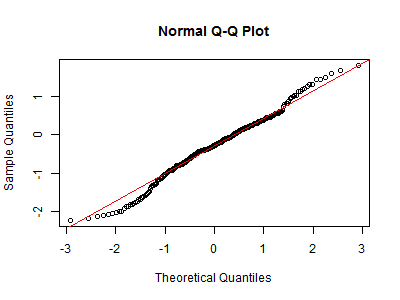
R Quantile-Quantile Plot Example


Quantile-Quantile plot is a popular method to display data by plot the quantiles of the values against the corresponding quantiles of the normal (bell shapes). The quantiles of the standard normal distribution is represented by a straight line. The normality of the data can be evaluated by observing the extent in which the points appear on the line. 

qqnorm(y, ...)
qqnorm(y, ylim, main = "Normal Q-Q Plot",xlab = "Theoretical Quantiles", ylab = "Sample Quantiles",plot.it = TRUE, datax = FALSE, ...)
qqline(y, datax = FALSE, ...)
qqplot(x, y, plot.it = TRUE, xlab = deparse(substitute(x)),
ylab = deparse(substitute(y)), ...)

x: The first sample for 'qqplot'
y: The second or only data sample
xlab, ylab, main: plot labels. The 'xlab' and 'ylab' refer to the y and x axes respectively if 'datax = TRUE'
plot.it: logical. Should the result be plotted?
datax: logical. Should data values be on the x-axis?
ylim: set limits of y axis

Following is a csv file example, we will draw a Quantile-Quantile plot of "Expression" values:


Let first read in the data from the file:

    > x <- read.csv("histogram.csv",header=T,sep="\t")
    > x <- t(x)
    > ex <- as.numeric(x[2,1:ncol(x)])
Draw a Quantile-Quantile plot:

    > qqnorm(ex)
    > qqline(ex,col="red")

The above plot shows that most of the data points are on or near the straight line, suggests that the data is almost normally distributed.

For further test of the data normality, we can check the mean and median of the dataset.

    > mean(ex)
     [1] -0.3053381
     > median(ex)
     [1] -0.29
Mean is the average of the values, and the median is the second quartile, when the data is normally distributed around the mean, then the mean and median should be equal. Since the mean and median above (-0.3053381 vs -0.29) are very close, so the data is seems quite symmetric.

We can write the plot into a file:

    > png("histogram3.png",400,300)
    > qqnorm(ex)
    > qqline(ex,col="red")
    > graphics.off()
convert.idontcarewhatyouthink.net © 2021  Terms of Use | Home